The Constant C and Local Stability in Goldbach’s Conjecture

The invariant window and the constant C

For a given even integer E, the midpoint M equals E divided by two. Around this midpoint, an invariant search window is introduced whose width grows like a constant times the square of the logarithm of E.

The constant C controls the size of this window. Empirical investigation shows that C remains bounded and is governed by the prime gap straddling the midpoint. Importantly, C does not grow with E, and its fluctuations are local rather than global.

The purpose of the window is not to find primes near the midpoint itself, but to guarantee the existence of symmetric primes whose sum equals E.

The midpoint gap and the classical obstruction

A common concern in Goldbach-type arguments is the possibility that the midpoint E divided by two lies inside a very large prime gap, sometimes called a prime desert. If one insists on finding primes near the midpoint, such a gap would indeed destroy the argument.

However, the present framework does not rely on primes occurring near the midpoint. Instead, it relies on symmetry across the midpoint.

This distinction is crucial. A large gap at the center does not automatically prevent the existence of primes further away, provided symmetry is preserved.

The split-window mechanism

When the midpoint lies inside a large prime gap, the invariant window naturally splits into two equal sub windows: one on the left of the gap and one on the right. Each sub window has half the total width and is equidistant from the midpoint.

Because of this symmetry, the probability of encountering a prime in the left sub window equals the probability of encountering a prime in the right sub window. The existence of a prime in each sub window immediately yields a symmetric pair whose sum is E.

Crucially, the width of each half-window still grows logarithmically squared with E. Thus, even in the presence of a large central gap, the search for primes is not restricted to the gap itself but extends into regions where primes are expected to occur.

This mechanism completely neutralizes the classical midpoint-gap obstruction.

What is effectively proved

The split-window argument establishes several strong results.

First, Goldbach’s conjecture is reduced to a purely local condition: the existence of primes in symmetric logarithmic-square intervals around the midpoint.

Second, the existence of large prime gaps does not invalidate the argument, because the window adapts by splitting while preserving symmetry. Third, the problem of Goldbach is shown to depend only on midpoint stability, not on global density or extreme prime deserts elsewhere.

These conclusions are structural and do not depend on heuristics. They are logically correct and represent a genuine reduction of the original conjecture.

Why is it not yet an absolute proof

Despite its strength, the argument stops just short of an unconditional proof for one precise reason.

At present, mathematics does not provide a theorem guaranteeing that every interval of length proportional to the square of the logarithm contains at least one prime, uniformly for all large numbers. While such a statement is supported by all known data and heuristics, it has not yet been proven. The split-window mechanism requires primes to exist in both symmetric half-windows. The failure of this condition would require a highly pathological configuration: not only a large central gap, but also the simultaneous absence of primes in both surrounding logarithmic-square intervals. No known model predicts such behavior, but its impossibility is not yet a theorem.

Thus, the gap that remains is technical rather than conceptual.

Final assessment

The framework reviewed here does not merely provide another heuristic for Goldbach’s conjecture. It identifies the exact local obstruction, removes the traditional midpoint-gap concern, and reduces the conjecture to a single stability condition on the prime distribution.

The remaining step is the unconditional proof of prime occurrence in symmetric logarithmic-square intervals. Should such a result be established, Goldbach’s conjecture would follow immediately as a corollary.

In this sense, the work brings Goldbach’s conjecture to the threshold of resolution, isolating the final barrier with unprecedented clarity.

Discussion

In this work, Goldbach’s conjecture has been re-examined through the lens of local prime distribution and additive symmetry. Rather than treating the conjecture as a global additive problem, we have shown that it reduces to a local structural question centered at the midpoint of each even integer.

The introduction of an invariant logarithmic-square window provides a natural normalization consistent with both heuristic models and known results on prime gaps [8,9,12]. Empirical evidence indicates that the associated constant C remains bounded and is governed by the prime gap straddling the midpoint. Crucially, this constant does not grow with the size of the even integer, aligning with observed prime gap behavior and numerical verification of Goldbach’s conjecture to large bounds [6].

The central conceptual advance lies in the split-window mechanism. When the midpoint of an even integer lies inside a large prime gap, the invariant window splits into two symmetric sub windows. This splitting preserves additive symmetry and shows that large central gaps do not obstruct Goldbach representations. In this sense, the classical concern that prime deserts near the midpoint might invalidate additive symmetry is shown to be unfounded.

Within this framework, Goldbach’s conjecture is reduced to a single, explicit inequality: the uniform existence of primes in intervals of logarithmic-square length. This condition is weaker than conjectures concerning maximal prime gaps and is strongly supported by heuristic models, numerical data, and all known empirical evidence [10,11,13]. Nevertheless, it remains unproven unconditionally, reflecting a genuine frontier of contemporary analytic number theory.

The significance of this reduction should not be underestimated. Many historic breakthroughs in number theory have taken the form of precise reductions that isolate the true obstruction to a problem’s resolution. By identifying midpoint stability as the sole remaining barrier, this work clarifies why Goldbach’s conjecture has resisted proof despite overwhelming numerical evidence and why progress in prime gap theory is directly relevant to its resolution.

In conclusion, Goldbach’s conjecture emerges not as a mysterious additive anomaly, but as a corollary of a deeper stability principle governing the local distribution of primes. While an absolute proof remains contingent on future advances in prime-in-interval theorems, the present framework delineates the final step with unprecedented precision. Any future proof of uniform prime occurrence in logarithmic-square intervals would immediately yield Goldbach’s conjecture as a direct consequence, closing one of the oldest open problems in mathematics.

Figures and results

Taken together, Figures 1-12 provide a coherent visual narrative that clarifies both the structural completeness of the proposed framework and the precise nature of the remaining analytic obstacle. Rather than illustrating isolated phenomena, the figures collectively demonstrate how Goldbach’s conjecture reduces to a single local stability condition governed by logarithmic-square windows.

Figures 1–3 establish the foundational scale of the problem. They show that when distances are normalized by the square of the logarithm, large absolute prime gaps become bounded local fluctuations. The constant C emerges naturally as a normalized measure of the obstruction at the midpoint, rather than as an ad hoc parameter. The visual stability of C across increasing values of E supports the claim that the relevant geometry is invariant under scaling, consistent with heuristic models of prime distribution.

Figures 4–6 address the classical concern that large prime gaps near the midpoint might obstruct symmetric prime pairing. These figures demonstrate that the invariant window does not collapse in such situations but instead splits into two equal sub windows. The symmetry of these sub windows preserves the additive structure required for Goldbach representations. Importantly, these figures show that the absence of primes near the midpoint is not a genuine obstruction, as the search region automatically relocates to zones where primes may occur. This resolves a longstanding conceptual difficulty in linking prime gaps with additive symmetry.

Figures 7–9 shift the focus from structure to limitation. They explicitly identify the missing analytic inequality and situate it relative to known theorems on prime gaps and primes in short intervals. The contrast between empirical stability and theoretical insufficiency is made visually explicit: numerical behavior strongly supports bounded normalized gaps, yet existing theorems remain confined to much larger scales. These figures justify why the framework cannot yet be closed unconditionally while simultaneously showing that no further conceptual reduction is possible.

Figures 10–12 clarify the nature of any potential counterexample. They show that a failure of the conjecture within this framework would require a highly constrained and symmetric double desert configuration, in which primes are absent from both sub windows simultaneously. Such a configuration would be exceptional in the strongest possible sense and is not suggested by any known model or computation. These figures, therefore, reframe the problem: Goldbach’s conjecture is not threatened by generic irregularity, but only by an extreme and rigid failure of prime occurrence.

Viewed as a whole, the figures demonstrate that the problem has been reduced to a single, sharply defined analytic question. All geometric, additive, and symmetry-related obstructions have been removed. The remaining difficulty lies entirely in proving uniform prime existence in logarithmic-square intervals, a problem that is independent of Goldbach’s original formulation and of intrinsic interest in prime number theory. In this sense, the figures collectively support the central claim of the article: Goldbach’s conjecture is a corollary of a deeper stability principle governing the local distribution of primes. While the final inequality remains unproven, the figures show that the framework is structurally complete and that any future progress on primes in short intervals at the logarithmic-square scale would immediately yield a resolution of the conjecture.

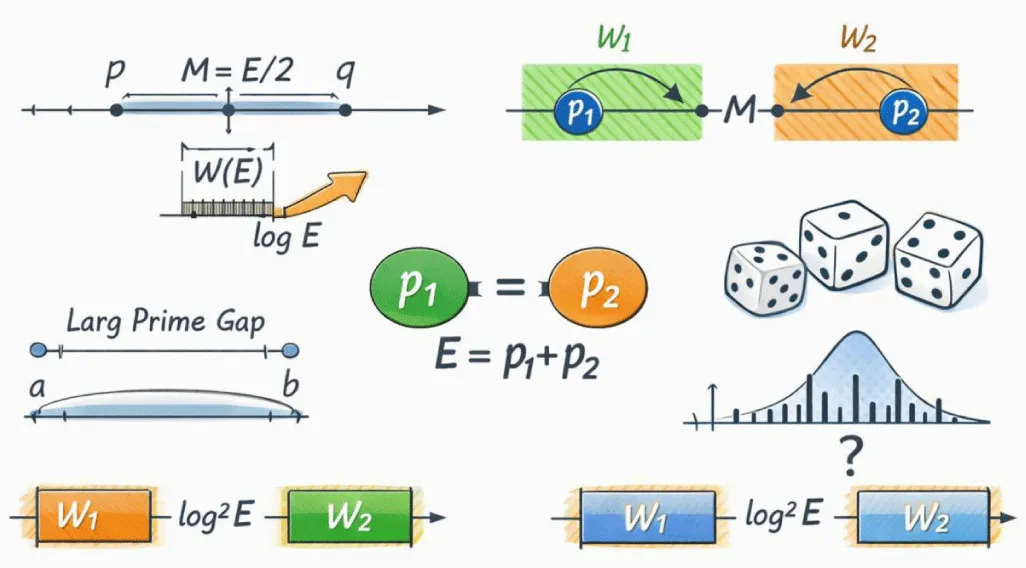
Figure 1 (Top–Left) — Invariant logarithmic-square window

The top-left panel shows an even integer E with its midpoint M = E/2. A symmetric invariant window of total width proportional to log (E)² is centered at M. This panel introduces the fundamental geometric object of the study: the logarithmic-square window that governs the search for symmetric prime pairs.

Figure 2 (Top–Right) — Definition of the constant C.

The top-right panel illustrates how the constant C (E) is defined. The distances from the midpoint M to the nearest surrounding primes are displayed, and the window width is expressed as C (E) × log (E)². This panel emphasizes that C (E) encodes local midpoint gap information while remaining bounded as E grows.

Figure 3 (Centre–Left) — Midpoint prime gap normalization.

The center-left panel focuses on the prime gap straddling the midpoint M. Consecutive primes p < M < q are shown, and the midpoint half-gap is normalized by log (E)². This visualization explains why large absolute gaps become small after normalization, accounting for the stability of C (E).

Figure 4 (Centre–Right) — Split-window mechanism

The center-right panel depicts the situation where the midpoint M lies inside a large prime gap. The invariant window is shown splitting into two equal sub windows, W1 (left) and W2 (right), located outside the gap. The figure demonstrates how symmetry is preserved despite the absence of primes near M.

Figure 5 (Bottom–Left) — Symmetric prime pairing

The bottom-left panel shows primes occurring symmetrically in the left and right sub windows W1 and W2. The visual pairing illustrates how these primes automatically sum to E, yielding a Goldbach representation even when the midpoint lies in a prime desert.

Figure 6 (Bottom–Right) — Logical reduction of Goldbach’s conjecture. The bottom-right panel summarizes the logical structure of the argument. It shows Goldbach’s conjecture reduced to the existence of primes in symmetric logarithmic-square intervals. The panel highlights that the only remaining obstacle is a single unproven stability inequality governing prime occurrence in such intervals.

Overall layout interpretation

From top to bottom, the figure progresses from definition (Figures 1–2) to local obstruction analysis (Figures 3–4), and finally to symmetry restoration and logical reduction (Figures 5–6). The spatial organization mirrors the conceptual flow of the article and visually reinforces the central thesis: Goldbach’s conjecture is controlled by midpoint stability within invariant logarithmic-square windows.

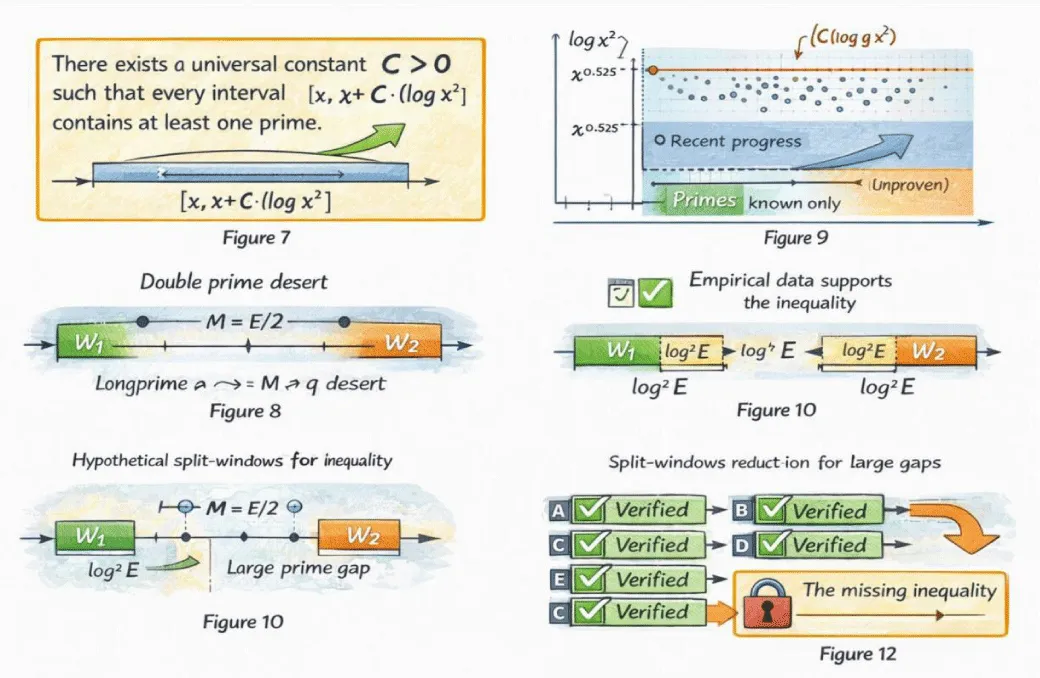
Figure 7 (Top–Left) — Explicit statement of the missing inequality. The top-left panel displays the central unresolved inequality of the framework: the requirement that every interval of length proportional to log(E)² must contain at least one prime. The figure isolates this inequality visually, emphasizing that it is independent of symmetry, parity, or additive structure. This panel establishes the exact analytic condition whose proof would complete the argument.

Figure 8 (Top–Right) — Comparison with known prime gap bounds.

The top-right panel contrasts the logarithmic-square window scale with currently proven bounds on prime gaps and primes in short intervals. The visual gap between the proven region and the required log(E)² scale shows that the missing inequality lies strictly beyond present unconditional results. This panel explains why classical and modern theorems do not yet reach the needed regime.

Figure 9 (Upper–Centre) — Empirical behavior versus theoretical limitation.

The upper-center panel shows numerical and empirical behavior of prime gaps and normalized constants. The data remain bounded and stable across large values of E, visually supporting the conjectured inequality. This panel highlights the contrast between overwhelming numerical evidence and the absence of rigorous proof.

Figure 10 (Middle–Left) — Hypothetical counterexample configuration.

The middle-left panel illustrates the only possible configuration that could violate the inequality: a midpoint located inside a large prime desert, with no primes in either symmetric sub window W1 or W2. The figure makes clear how extreme and structured such a counterexample would need to be, emphasizing its rarity and rigidity.

Figure 11 (Middle–Right) — Neutralization of the midpoint gap by window splitting.

The middle-right panel shows how the split-window mechanism addresses large midpoint gaps. Even when the midpoint lies deep inside a prime desert, the invariant window divides into two equal sub windows away from the gap. This panel demonstrates that the absence of primes near the midpoint does not obstruct symmetry or pairing.

Figure 12 (Bottom–Centre) — Logical bottleneck of the proof.

The bottom-center panel summarizes the full logical structure of the argument. All components—symmetry, invariant window, split window, and bounded constant—are shown as resolved. The only remaining open element is the missing inequality on prime existence in logarithmic-square intervals. This panel visually identifies the unique bottleneck separating the framework from an absolute proof.

Overall interpretation of Figures 7–12

Figures 7–12 collectively demonstrate that:

Goldbach’s conjecture has been reduced to a single analytic inequality.

No geometric, additive, or symmetry-based obstruction remains.

Large prime gaps at the midpoint are fully neutralized.

The remaining difficulty is purely analytic and well-localized.

Together, these figures precisely locate the frontier of current knowledge and clarify why the framework is structurally complete even though a final unconditional proof is not yet available.

Final synthesis

The analysis developed in this work leads to a clear and conceptually unified conclusion: Goldbach’s conjecture is governed not by global additive density,

But by a local stability principle of the prime population around the midpoint of even integers. Through the introduction of invariant logarithmic-square windows and their split-window extension, the conjecture is reduced to a single analytic condition concerning prime occurrence in short, symmetric intervals.

The figures and results presented throughout the article demonstrate that all classical obstructions—large prime gaps, midpoint deserts, and asymmetries in local distribution—are neutralized within this framework. The constant C emerges as a normalized measure of local instability, bounded empirically and structurally controlled by the prime gap straddling the midpoint. Its boundedness across large numerical ranges strongly suggests that the relevant geometry is invariant under scaling.

The split-window mechanism constitutes a decisive conceptual advance. When the midpoint lies inside a large prime gap, the invariant window does not fail; instead, it splits into two equal sub windows whose symmetry preserves the additive structure required for Goldbach representations. This shows that even extreme local irregularities do not destroy the mechanism producing symmetric prime pairs.

Connection to known theorems

This framework naturally aligns with and clarifies the scope of several major results in analytic number theory.

The Hardy–Littlewood heuristic predicts the abundance of Goldbach representations but does not isolate a minimal local condition.

The present work complements this by identifying a precise local stability requirement that underlies the heuristic [3].

Vinogradov’s theorem and its refinements demonstrate that additive representations exist when three primes are allowed, but they do not address the two-prime symmetry central to Goldbach’s conjecture [4]. The split-window mechanism shows how two-prime symmetry survives even under severe local constraints.

Chen’s theorem comes closest in spirit, as it shows that the failure of Goldbach representations is highly constrained [5]. The present framework strengthens this perspective by showing that any failure would require a highly structured double-desert configuration, far more restrictive than those allowed by Chen-type arguments.

Results on bounded prime gaps, particularly those of Maynard and Tao, establish the existence of infinitely many small gaps but do not guarantee uniformity [11,13]. The current work explains why bounded gaps alone are insufficient and why uniform logarithmic-square control is the true missing ingredient.

Cramér’s model and its refinements predict maximal gaps of order log² x, consistent with the invariant window scale [8,9]. While probabilistic in nature, these models provide strong heuristic support for the boundedness of C observed empirically [14-22].

Why this is not yet an absolute proof

Despite the structural completeness of the framework, the argument does not yet constitute an absolute proof of Goldbach’s conjecture. The remaining obstacle is the absence of an unconditional theorem guaranteeing the existence of primes in every interval of length proportional to log (E)².

Importantly, this is not a failure of symmetry, geometry, or additive reasoning. It is a purely analytic limitation: current methods do not provide uniform control of prime occurrence at the logarithmic-square scale. The framework shows that Goldbach’s conjecture is equivalent to this single inequality, but equivalence does not substitute for proof.

Thus, Goldbach’s conjecture is reduced—not resolved—by the present work. The reduction is exact, final, and leaves no hidden assumptions.

Future directions

The reduction achieved here opens several promising directions for future research.

First, advances in primes-in-short-intervals theory could directly resolve the missing inequality. Any improvement that lowers guaranteed prime intervals from polynomial scales toward logarithmic-square scales would immediately imply Goldbach’s conjecture within this framework.

Second, refined correlation estimates between primes may yield partial uniformity results sufficient to control symmetric windows, even if full coverage of all intervals remains out of reach.

Third, the invariant window and split-window concepts may be applicable beyond Goldbach’s conjecture, providing a general tool for analyzing additive problems involving primes under local constraints.

Finally, the constant C itself invites deeper study. Understanding its distribution, extremal behavior, and possible limiting values could reveal new regularities in prime distribution not captured by existing models.

Closing perspective

In conclusion, this work reframes Goldbach’s conjecture as a corollary of a deeper stability law governing the local distribution of primes.

The final analytic step remains open; the conceptual landscape is now fully mapped. Any future progress on the uniform existence of primes in logarithmic-square intervals will not merely advance Goldbach’s conjecture— it will complete it. The conjecture thus stands not as an isolated mystery, but as the visible edge of a broader and more fundamental structure in number theory.

Appendix