Thermodynamic Analysis of Ammonia Synthesis

The paper researches the effect of temperature on ammonia synthesis. The ammonia synthesis reaction $N_2{}_{(g)}+3H_{2(g)}=2N{H}_{3(g)}$ is exothermic with a negative entropy change. ∆G < 0 condition is fulfilled at lower temperatures up to 464K (Le Chatelierov principle). It is a constant equilibrium of the ammonia synthesis reaction $K_p\text{'}>>1$ at lower temperatures, which means that the NH_3(g) synthesis reaction is shifted in the direction of NH_3(g) formation (higher production of ammonia). The downside of lowering the temperature is that more ammonia is obtained, but the reaction rate slows down. Above 464K, the free enthalpy of the NH_3(g) synthesis reaction is greater than zero, so the reaction enters thermodynamically unfavorable conditions. By increasing the reaction temperature, the ammonia yield NH_3(g) decreases in the equilibrium mixture. At 400K, it is 0.5127kmol/kmol (51.27%) and at 700K, the synthesis process NH_3(g) is practically complete.

Introduction

Ammonia is a colorless gas with a pungent odor. It dissolves well in water. At ambient temperature, ammonia NH_3(g) is stable. Ammonia is mainly used for the production of nitric acid and mineral fertilizers, carbamide, ammonium sulfate, and others. Ammonia gas reacts quickly with sulfuric acid vapors SO_3(g) and H₂O(_g) creates ammonium sulfate ${(N{H}_4)}_{2}S{O}_4{}_{\left(s\right)}$ which is a high-quality artificial fertilizer. Gaseous ammonia is also used for the reduction of SO_3(g) and NO_x(g) in flue gases, and the reduction ranges from 77% - 97% [1]. In the literature [2-7] there are data on the synthesis of ammonia

$N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}.\text{ (1)}$

These data are not complete. They relate to a certain temperature and pressure. Data on the effect of temperature on the composition of the equilibrium reaction mixture (1) are also incomplete. In engineering practice, the Haber-Bosch process is most often used for the production of ammonia [8,9].

Knowledge of the value of thermodynamic functions ∆H, ∆S, ∆G and K_p, as well as knowing the composition of the equilibrium reaction mixture (1) is the starting point in the design phase of devices and apparatus for the reduction of sulfur and nitrogen oxides in flue gases, the production of mineral fertilizers and polymer materials, which gives significance to this paper.

The enthalpy of a chemical reaction is defined as follows [10,11]:

$\Delta H={\displaystyle \sum _j{b}_j\cdot \Delta h_j}-{\displaystyle \sum _i{b}_i\cdot \Delta h_i}\text{ (2)}$

of which :

b_i - the number of kilomoles of the i-th reactant components.

b_j - the number of kilomoles of the j-th component for products.

∆h_i - bond enthalpy of the i-th component.

∆h_j - bond enthalpy of the j-th component.

The dependence of reaction enthalpy on temperature is given by the expression:

$\Delta H_T=\Delta H_{298}+{\displaystyle \underset{298}{\overset{T}{\int }}\Delta c_{mp}(T)dT}\text{ (3)}$

of which:

$\Delta c_{mp}={\displaystyle \sum _j{b}_j\cdot c_{mp}{}_j}-{\displaystyle \sum _i{b}_i\cdot c_{m{p}_i}}.\text{ (4)}$

and represents the sum of the specific molar heat capacities of the components.

The dependence of molar heat capacity on temperature can be shown in the form of a polynomial:

$c_{mp}(T)=a+b\cdot {10}^{-3}\cdot T+c\cdot {10}^5\cdot T^{-2}\text{ (5)}$

of which:

a,b,c - polynomial coefficients that are determined experimentally.

T - absolute temperature.

The entropy of a reaction is defined by the expression:

$\Delta S={\displaystyle \sum _j{b}_j\cdot s_j}-{\displaystyle \sum _i{b}_i\cdot s_i}\text{ (6)}$

of which:

si - specific entropies and connections of the i-th component.

sj -specific entropies and connections of the j-th component.

The dependence of reaction entropy on temperature is given by the expression:

$\Delta S_T=\Delta S_{298}+{\displaystyle \underset{298}{\overset{T}{\int }}\frac{\Delta c_{mp}(T)}{T}dT}\text{ (7) }$

The free enthalpy of reaction is defined by the expression:

$\Delta G={\displaystyle \sum _j{b}_j\cdot \Delta g_j}-{\displaystyle \sum _i{b}_i\cdot \Delta g_i}\text{ (8)}$

of which:

∆gi - specific free enthalpies of the i-th component.

∆gj -specific free enthalpies of the j-th component.

The dependence of the free reaction enthalpy on the reaction enthalpy, temperature, and entropy of the reaction is given by the expression:

$\Delta G=\Delta H-T\cdot \Delta S\text{ (9)}$

If the reaction ∆G > 0 proceeds from right to left, i.e. in the direction of the formation of the reaction reactants.If reaction ∆G < 0 proceeds from left to right, i.e. in the direction of the formation of reaction products.

For a chemical reaction:

${\displaystyle \sum _i{a}_i\cdot A_i}={\displaystyle \sum _j{b}_j\cdot B_j}\text{ (10)}$

the chemical equilibrium constant expressed through partial pressures is:

$K_p=\frac{{\displaystyle \prod _j{(p_{B_j})}^{b_j}}}{{\displaystyle \prod _i{(p_{A_i})}^{a_i}}}.\text{ (11)}$

The value of the chemical equilibrium constant ${K^{\prime }}_p$ reduced to pressure $p_0=1.013\cdot {10}^5\text{Pa}$ is determined by the expression:

$K_p{}^{\prime }=e^{-\frac{\Delta G}{R_u\cdot T}}=K_p\cdot p_0{}^{-({\displaystyle \sum _j{b}_j-{\displaystyle \sum _i{a}_i)}}}\text{ (12)}$

of which:

$R_u=8.314\frac{\text{kJ}}{\text{kmolK}}$ – universal gas constant.

Using numerical thermodynamic data for pure components that figure in the reaction $N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$ at $298K$ and 1.013.10⁵ Pa (Tables 1,2) and using expressions from (2) to (12), it is possible to calculate the thermodynamic functions ∆H, ∆S, ∆G, K_p′ of the considered reaction depending on the reaction temperature.

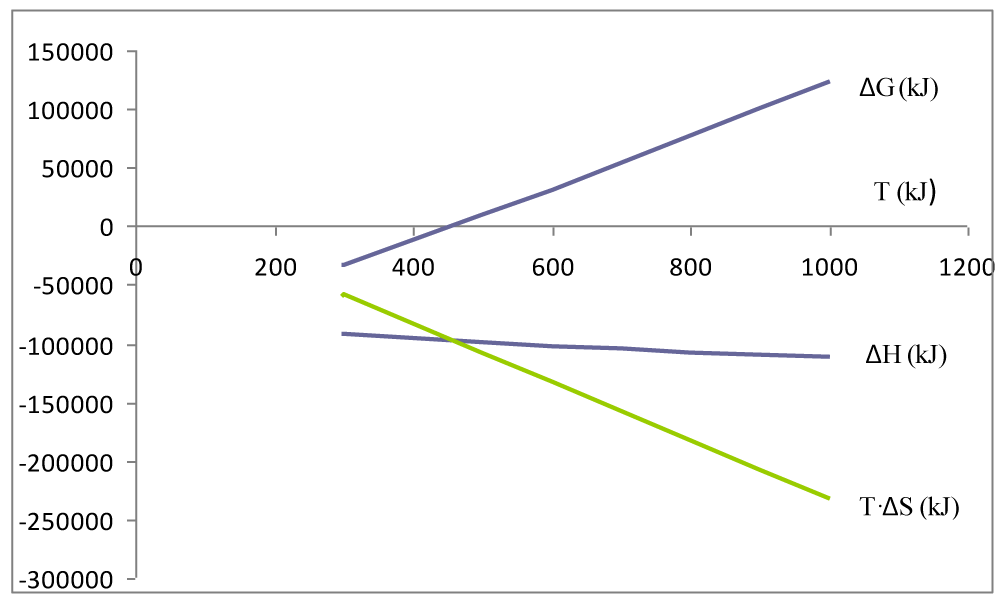
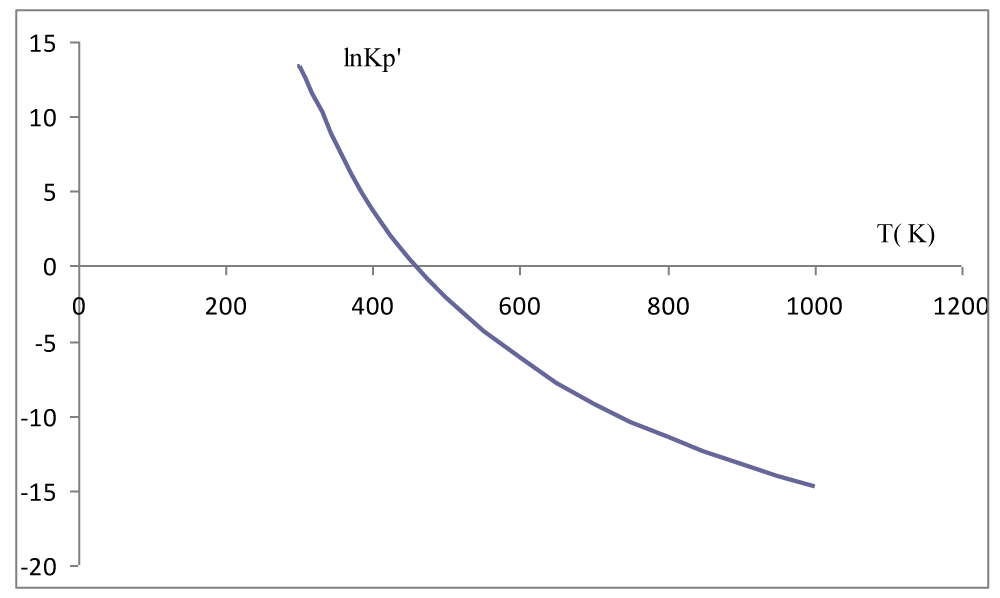
The results of the calculation of the thermodynamic functions ∆H, ∆S, ∆G, K_p′, K_p are shown in Table 3. In the temperature interval 298K to 1000K, the thermodynamic functions and are negative, so the sign ∆G is determined by the relative ratio of the enthalpy and entropy terms (equation (9)) (Figure 1). This means that reaction temperature is a decisive factor for the thermodynamic balance of the synthesis reaction NH_3(g). In the temperature interval of 298K to 464K, the equilibrium constant of the considered reaction is very large K_p′ >> 1, which means that the reaction is shifted in the direction of product formation NH_3(g). At a reaction temperature above 464K, the chemical equilibrium constant K_p′ << 1, so the equilibrium of the reaction shifts in the direction of the formation of reactants of the reaction (Figure 2).

Figure 1: Determination of the reaction area for an exothermic reaction $N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$ depending on the reaction temperature.

Figure 2: Dependence of the reaction equilibrium constant $N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$ from the temperature.

Calculation of the composition of the equilibrium mixture of the synthesis reaction NH_3(g)

Balance equations of reactants in the reaction:

$N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}\text{ (13)}$

can be written as follows:

$\text{nitrogen }{n}_{N_{2(g)}}=a-y,\text{(kmol) (14)}$

$\text{hydrogen }{n}_{H_{2(g)}}=b-3y,\text{(kmol) (15)}$

$\text{ammonia }{n}_{N{H}_{3(g)}}=2y,\left[kmol\right]\text{ (16)}$

of which:

a - the number of kilomoles of nitrogen entering the reaction (13).

b - the number of kilomoles of hydrogen reacting (13).

2y - the number of kilomoles of ammonia in the mixture after establishing chemical equilibrium.

The total number of kilomoles in the mixture at any conversion time is equal to:

$n_{\sum }=n_{{\text{N}}_{\text{2}}\text{(g)}}+n_{{\text{H}}_{\text{2}}\text{(g)}}+n_{{\text{NH}}_{\text{3}}\text{(g)}}$

$n_{\sum }=(a-y)+(b-3y)+2y=a+b-2y\text{ (17)}$

The mole fraction of the components in the mixture after the establishment of chemical equilibrium amounts to:

$y_{N_2(g)}=\frac{n_{N_2(g)}}{n_{\sum }}=\frac{a-y}{a+b-2y},\text{(kmol/kmol) (18)}$

$y_{H_2(g)}=\frac{n_{H_2(g)}}{n_{\sum }}=\frac{b-3y}{a+b-2y},\text{(kmol/kmol) (19)}$

$y_{N{H}_3(g)}=\frac{n_{N{H}_3(g)}}{n_{\sum }}=\frac{2y}{a+b-2y},\text{(kmol/kmol) (20)}$

The partial pressures of the components in the equilibrium mixture are:

$p_{N_2(g)}=y_{N_2(g)}\cdot p=\frac{a-y}{a+b-2y}\cdot p,\text{(Pa) (21)}$

$p_{H_2(g)}=y_{H_2(g)}\cdot p=\frac{a-3y}{a+b-2y}\cdot p,\text{(Pa) (22)}$

$p_{N{H}_3(g)}=y_{N{H}_3(g)}\cdot p=\frac{2y}{a+b-2y}\cdot p,(\text{Pa) (23)}$

of which:

p - total pressure in the reactor space after equilibrium is established, (Pa).

The chemical equilibrium constant of the reaction (13) is determined using the expression:

$K_p=\frac{p_{N{H}_3(g)}{}^2}{p_{N_2(g)}\cdot p_{H_2(g)}{}^3},({\text{Pa}}^{\text{-2}})\text{ (24)}$

By changing equations (21) to (23) into equation (24) and solving for the unknown y the equation is obtained:

$A{y}^4+B{y}^3+C{y}^2+Dy+E=0\text{ (25)}$

of which:

$A=27p^2{K}_p-16$

$B=(a+b)\cdot (16-27p^2{K}_p)$

$C=9b{p}^2{K}_p\cdot (b+3a)-4\cdot {(a+b)}^2$

$D=-b^2{p}^2{K}_p\cdot (9a+b)$

$E=a{b}^3{p}^2{K}_p$

By substituting the solution of equation (25) into expressions (21) to (23), the numerical values of the mole fractions of the components in the equilibrium mixture are obtained. The degree of responsiveness of reactants N_2(g) and H_2(g) is determined using the expression:

${\eta }_{N_2(g)}=\frac{a-(a-y)}{a}=\frac{y}{a},\text{(kmol/kmol) (26)}$

${\eta }_{H_2(g)}=\frac{b-(b-3y)}{b}=\frac{3y}{b},\text{(kmol/kmol) (27)}$

The results of the calculation of the composition of the equilibrium mixture of the reaction

$N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$

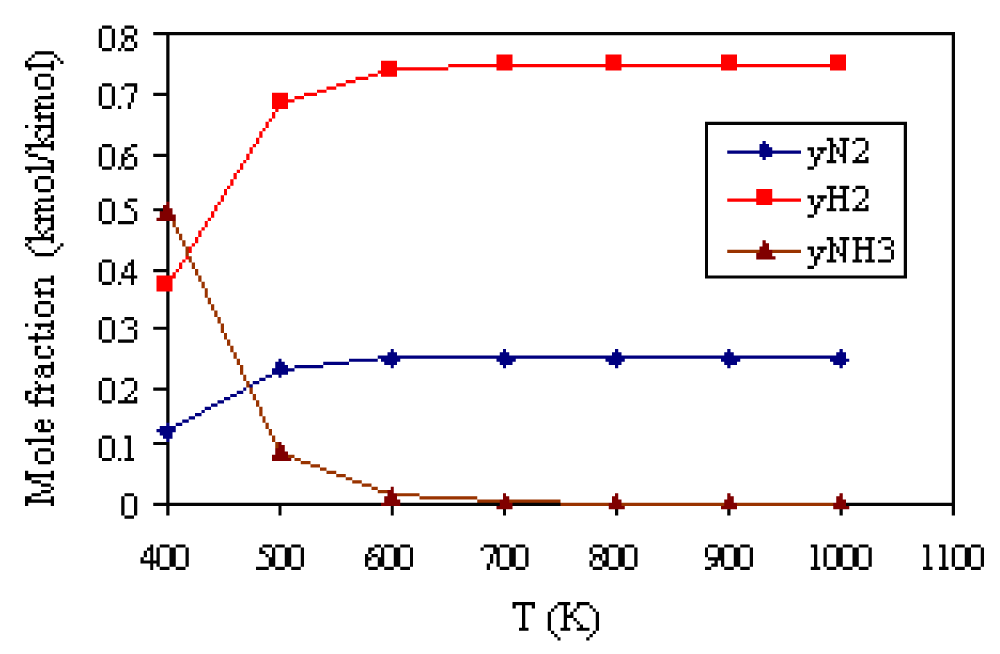
The results of the calculation of the composition of the equilibrium mixture at the stoichiometric ratio of reactants, at T = 400K, and pressure p = 1.013 · 10⁵ Pa are shown in Table 4, and the graphic dependence in Figure 3.

Figure 3: Mole fraction of components in the equilibrium reaction mixture $N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$ depending on the temperature

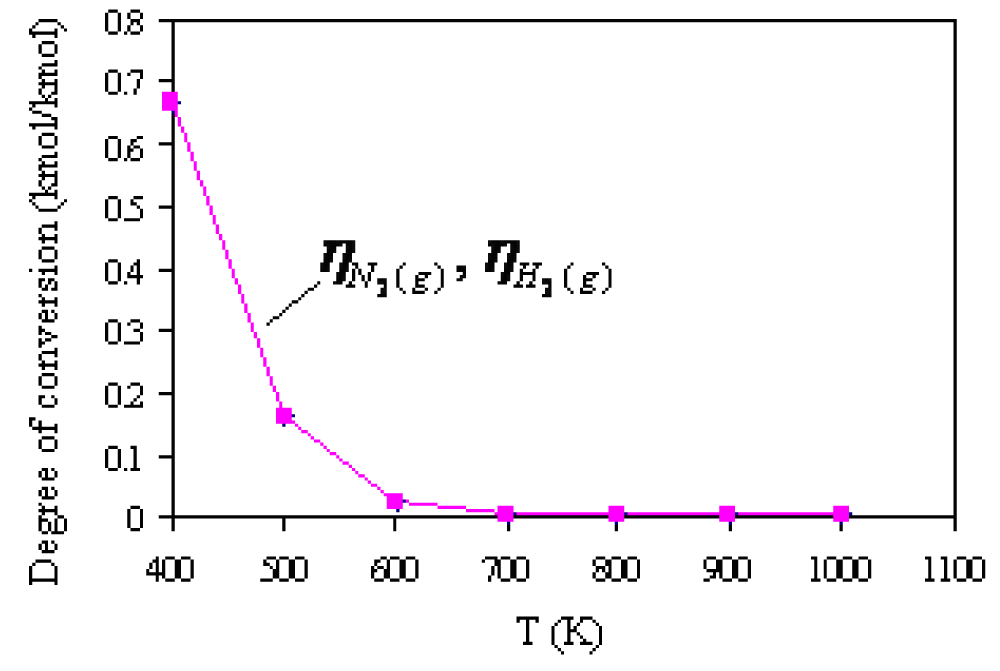
It can be seen that ammonia synthesis starts at lower temperatures. At 400K, the mole fraction of ammonia in the equilibrium mixture is 0.50 kmol/kmol. At higher temperatures, the mole fraction of ammonia decreases, while at 700K, the mole fraction of ammonia is practically equal to 0. The degree of conversion (reaction) N_2(g) and H_2(g) depending on the temperature is shown in Figure 4. Apparently, the increase in the reaction temperature and mole fraction shares N_2(g) and H_2(g) in the equilibrium reaction $N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$ mixture, the degree of conversion of the reactants decreases. At 400K, the degree of conversion of reactants is as much as 0.67 kmol/kmol, and at 700K, the degree of conversion is practically 0 kmol/kmol. This practically means that the synthesis process NH_3(g) at 700K is completed because it amounts to only 0.0029 kmol/kmol.

Figure 4: Degree of conversion H_2(g) H_2(g)N_2(g) and H_2(g) in the equilibrium reaction mixture $N_{2(g)}+3H_{2(g)}=2N{H}_{3(g)}$ depending on the temperature.

Conclusion

The paper presents the thermodynamic analysis of ammonia synthesis and the following conclusions were reached:

• The ammonia synthesis reaction is exothermic with a negative entropy change in the temperature interval of 298-1000K;
• The sign of the free enthalpy of the  $\Delta G$ reaction is determined by the ratio of the enthalpy and entropy term (equation (9)), which means that the reaction temperature is a decisive factor for the thermodynamic balance of the synthesis reaction NH_3(g);
• Constant balance reactions synthesis of ammonia is much larger than 1(K_p′ >> 1) at lower temperatures which means that the reaction synthesis continued in a construction direction. Above 464K, a free synthesis reaction enthalpy is higher than zero, thus, the reaction enters the thermodynamic unfavorable conditions;
• By increasing the reaction temperature, the ammonia yield in the equilibrium mixture decreases. At 400K it amounts to 0.5127kmol/kmol (51.27%) and at 700K, the synthesis process is practically finished;
• Due to the slow speed of the ammonia synthesis reaction, industrial catalysts are used in practice to achieve sufficient activity at higher temperatures (> 464K).

This paper can be used as the initial basis of phase designing devices and apparatus in various branches of procedural techniques, and chemical engineering as well as for a better understanding of the process of combustion and synthesis of the multicomponent systems.

Further research into ammonia synthesis should be directed at determining the speed of the considered reaction. It is also necessary to investigate the influence of different industrial catalysts on the speed of the ammonia synthesis reaction.

1. Đurić NS, Đaković DD. Improving the energy and environmental efficiency of thermal power plants by lowering the dew point temperature of flue gases. Termotehnika. 2010;XXXVI(2-3):233-245. (In Serbian: Unapređenje energetske i ekološke efikasnosti termoelektrana snižavanjem temperature tačke rose dimnih gasova).
2. Cui P, Zhou Y, Song T, Xu Z, Zhang J, Liu Y, et al. Thermodynamic and economic analysis of an ammonia synthesis process integrating liquified natural gas cold energy with carbon capture and storage. ACS Sustainable Chem Eng. 2023;11(7):1-6. Available from: https://doi.org/10.1021/acssuschemeng.2c06841
3. Kim H, Oh S, Mun H, Kim D, Lee I, Moon IL. Advanced design of ammonia production processes from LNG: Efficient and economical cold energy utilization methods. Ind Eng Chem Res. 2023;62(19):7566-7579. Available from: https://doi.org/10.1021/acs.iecr.3c00058
4. Christiansen LJ. Thermodynamic properties in ammonia synthesis. Berlin: Springer-Verlag; 1995. Available from: https://link.springer.com/chapter/10.1007/978-3-642-79197-0_1
5. Schlögl R. Ammonia synthesis. Berlin: Fritz-Haber-Institute of the MPG; 14195 Berlin. Available from: https://pure.mpg.de/rest/items/item_736938_6/component/file_932945/content
6. Shamiri A, Aliabadi N. Modeling and performance improvement of an industrial ammonia synthesis reactor. Chem Eng J Adv. 2021;8:100177. Available from: https://doi.org/10.1016/j.ceja.2021.100177
7. Karavaev MM, Zasorin AP, Klešeev NF. Katalitičeskoe okislenie ammiaka. Moscow: Himija; 1983.
8. Navid, Luqmanulhakim B, Matthew W. Recent advances and intensifications in Haber-Bosch ammonia synthesis process. Chem Eng Process Process Intensif. 2024;204:109962. Available from: https://doi.org/10.1016/j.cep.2024.109962
9. Wei Q, Lucero JM, Crawford JM, Way JD, Wolden CA, Carreon MA. Ammonia separation from N2 and H2 over LTA zeolitic imidazolate framework membranes. J Membr Sci. 2021;623:119078. Available from: https://doi.org/10.1016/j.memsci.2021.119078
10. DeVoe H. Thermodynamics and Chemistry [Internet]. 2nd ed. Version 10. College Park, Maryland: University of Maryland; 2020. Available from: https://www2.chem.umd.edu/thermobook/v10-screen.pdf
11. Kuo J. Chemistry, Thermodynamics, and Reaction Kinetics for Environmental Engineers. 1st ed. 2025. Available from: https://doi.org/10.1201/9781003502661
12. Johnson DA. Some thermodynamic aspects of inorganic chemistry. Cambridge: Cambridge University Press; 1982. Available from: https://www.cambridge.org/in/universitypress/subjects/chemistry/chemistry-general-interest/some-thermodynamic-aspects-inorganic-chemistry-2nd-edition?format=PB&isbn=9780521285216
13. Barin I, Knacke O. Thermochemical Properties of Inorganic Substances. Berlin-Heidelberg-New York: Springer-Verlag; 1973. Available from: https://www.springer.com/series/2212?srsltid=AfmBOoou1vz4BcMaYwUvCqMsuMgtlIqCgzKd-CbdoamUr88Tbmf2jIWw